Racine cubique

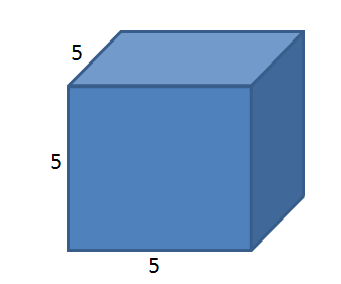
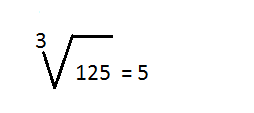Avant de comprendre ce qu'est la racine cubique, vous devriez comprendre ce qu'est le cube.
Le cube est la puissance troisième d'un nombre.
Par exemple le cube de 5 est:
5×5×5=125

Le cube de 5 est 5×5×5 = 125
Le cube de 5 s’écrit 5³ (le petit "³" signifie qu'il faut multiplier le nombre 3 fois par lui-même.

Quelques cubes:
Le cube de 4= 4³ =4×4×4=64
Le cube de 6= 6³ =6×6×6=216


La racine cubique:

La racine cubique d'un nombre réel X est l'unique nombre réel Y qui, élevé à la puissance 3 vaut X ; en d'autres termes, X = Y³.

la racine cubique de 64 est 4, parce que 4³=64
la racine cubique de 216 est 6 parce que 6³=216

Le symbole de la racine cubique est:
La racine cubique de X est notée:

Le symbole spécial qui signifie «racine cubique», c'est le symbole «radicale» (utilisé pour les racines carrées) avec un petit trois pour signifier racine cubique.



Vous pouvez l'utiliser comme ceci: racine cubique de 125 = 5 (vous diriez «la racine cubique de 125 est égale à 5")

Formules de géométrie, aire

Vous trouverez dans cette partie, des formules de géométrie pour l'aire des figures les plus communes:

Exemple:

A) Calculer l'aire du triangle sachant que b= 8cm et h= 4cm

Selon la formule de géométrie
L'aire du triangle est (b x h)/2 = 16cm²

B) Calculer l'aire du rectangle avec L= 10 cm    l=5cm

Selon la formule de géométrie:
L'aire du rectangle est L x l = 50cm²

C) Calculer l'aire du trapèze sachant que a=3 cm   b=7 cm    h=2,5 cm

Selon la formule géométrique:
L'aire du trapèze est 1/2(a+b) x h = 5cm x 2,5cm= 12,5cm²

D) Calculer l'aire du carré de 4cm de côté

Selon la formule géométrique:
L'aire du carré est a²   avec a=côté
Aire du carré est 16cm²

E) Calculer l'aire du parallélogramme ayant comme base b 10cm et comme hauteur h 3cm

Selon la formule géométrique:
L'aire du parallélogramme est b x h = 30cm².


F) Calculer l'aire du cercle ayant comme rayon 4cm

Selon la formule géométrique:
L'aire du cercle est πr²= 50,26cm².

Calculer la circonférence d'un cercle

La circonférence d'un cercle est la longueur de la ligne extérieure du cercle. On pourrait l'appeler le périmètre du cercle.

Pour calculer la circonférence d'un cercle, vous devez utiliser la formule suivante: C=πd.

C= la circonférence ou le périmètre du cercle
d= c'est le diamètre du cercle
π (pi). Sa valeur n'est pas finie, et peut être approchée par 3,141 592 654, arrondie à 10^-9.


Exemple:
Soit un cercle de 8cm de diamètre

Calculer la circonférence du cercle.


Selon la formule de la circonférence du cercle C=πd.
C=8π= 25,13 (en utilisant une calculette).

S'il vous est donné uniquement le rayon pour le calcul du périmètre du cercle, rappelez-vous que le diamètre est deux fois plus grand que le rayon (2r=d).

Comment calculer des intérêts composés

Avant de déterminer comment calculer des intérêts composés, nous allons expliquer brièvement ce que c'est.

Les intérêts composés sont calculés non seulement sur le capital mais aussi sur les intérêts accumulés sur les périodes précédentes, contrairement aux intérêts simples.

Exemple:
Ce tableau présente un prêt à intérêts composés sur 5 ans.
Le capital emprunté en début de période (période 0) est 10000€ avec un taux d'intérêts composés de 10%.

Les intérêts représentent les intérêts sur chaque période.

Période	Prêt en début de période	Intérêts	Prêt en fin d'année
0 (maintenant)	10000	10000 x 10% = 1000€	11000€
1	11000€	11000 x 10% =1100€	12100€
2	12100€	12100 x 10% = 1210€	13310€
3	13310€	13310 x 10% = 1331€	14641€
4	14641€	14641 x 10% = 1464,1€	16105,1€
5	16105,1€

Si vous procédez par étape avec un tableau, le calcul des intérêts composés est assez facile à réaliser,
Il faut prendre la valeur du prêt en fin d'année, qui servira de base pour calculer les intérêts de l'année en cours...et ainsi de suite pendant toute la durée du prêt.

mais il existe une formule que vous pouvez utiliser et qui simplifiera les calculs:

Capital x (1 + taux pour la période) ^ Nombre de périodes = Capital en fin de période

Dans notre exemple:
10000 x (1+0.1)^5=16105,1€
16105,1€ est le prêt total à rembourser après les 5 ans.


En conclusion, le calcul des intérêts composés peut être obtenu soit en utilisant le tableau (qui sur une longue période peut être long à faire) ou soit en utilisant la formule précédente.
Il serait intéressant aussi de lire l'article sur les intérêts simples juste pour votre information personnelle.

Comment calculer des intérêts

Voici comment calculer des intérêts simples:

Voici l'une des formules permettant de déterminer l'intérêt acquis au bout d'une période n:

C * t * n= I
avec C= capital
t= taux d'intérêt
n= nombre de périodes de placements (années, semestres...)
I=intérêt acquis

Le capital est le montant sur ​​lequel les intérêts sont calculés, le taux est le taux d'intérêt sous forme de pour cent et la période est le temps sur lequel l'intérêt est calculé.


Exemple:
Si un capital de 100000 euros est placé au taux de 4% (taux d'intérêt simple) par an pendant 8 ans, calculer le montant total des intérêts au bout de 8 ans?


Selon la formule précédente:
100,000€ X 0.04(taux de 4%) X 1 année (période) = 4000€ (montant d'intérêt pour une année)

4000*8= 32000€ montant total d'intérêt au bout de la 8ième année.

Une autre formule permet d'avoir de calculer le montant total du capital au bout de la nième année:
C X {1 + (taux X période)} = Capital à la fin de la période 1
100000€ X {1 + (0.04 X 1)} = $100,000 X 1.04 = 104000€

Sur 8 ans le montant total du capital est:
100000€ X {1 + (0.04 X 8)} = $100,000 X 1.32 = 132000€


Au bout de 8 ans le montant total des intérêts acquis est 32000€:
132000€-100000€ =32000€.


L'intérêt simple est très limité et est rarement utilisé tel quel, il existe d'autres formes d'intérêts comme les intérêts composés, qui sont utilisés plus régulièrement.
L'intérêt simple est utile car il permet d'avoir des connaissances basiques sur la façon de calculer des intérêts.

Comment calculer le diamètre d'un cercle

Pour calculer le diamètre d'un cercle, vous pouvez utiliser différentes formules dépendant des données à votre disposition.

Un cercle est l'ensemble de tous les points d'une courbe plane fermée, situés à une distance fixe, appelé le rayon, à partir d'un point donné, le centre.

Aire du cercle= πr²
Diamètre du cercle (d)= 2r
Longueur du cercle = 2πr = πd

Avec r = rayon
d = diamètre
Π= 3,14159265358979....

Exemples:

A) Calculez la diamètre du cercle C sachant que le rayon r= 5cm

Selon la formule précédente d=2r
Dans ce cas d= 10cm

B) Calculez le diamètre d du cercle C sachant que la longueur du cercle=23,75 cm

Selon la formule précédente: la longueur du cercle= 2πr = πd
avec π = 3.14....

Donc 23,75= πd
d =23,75/π
d =7,56 cm.

C) Calculez le diamètre d du cercle sachant que l'aire du cercle= 34cm2

Selon les formules données précédemment
-l'aire du cercle= πr²
-d = 2r

πr²= 34cm2
r²= 10,82cm2
r= 3.29cm

d=2r d=6.58 cm

Comment calculer le périmètre d'un triangle

Dans cet article, vous apprendrez comment calculer le périmètre d'un triangle de façon simple:


Il suffit d'additionner les longueurs des différents côtés du triangle.

A+B+C= périmètre du triangle


Exemple:
Calculer le périmètre d'un triangle
A= 5cm
B= 5cm
C= 4cm

Le périmètre de ce triangle est:
A+B+C= 24cm.

Il faut aussi s'assurer que les différentes mesures sont données dans la même unité de mesure, sinon vous devrez faire une conversion au préalable.
N'oubliez surtout pas d'ajouter l'unité de mesure à la fin du calcul du périmètre du triangle.

Comment calculer l'âge moyen

Si vous faites partie d'un groupe et voulez calculer l'âge moyen du groupe, voici une méthode à utiliser:

1- Il vous faut connaitre la date de naissance de chaque personne, et calculer l'âge de chaque personne.

2- Vous devez savoir combien de personnes ont le même âge (si vous avez des effectifs faibles (inférieur à 2) pour des personnes ayant le même âge, vous pouvez sauter cette étape et passer à l'étape 3b).

3- Calculer l'âge moyen:
*a) En cas de grands effectifs (méthode plus simple et rapide)
(somme (âge * nombre de personnes ayant cet âge)) / nombre total de personnes du groupe (N)

*b) Calcul d'une moyenne simple (ici dans le cas du calcul de l'âge moyen du groupe):
Total des âges/ effectif total (N)

Les deux méthodes donnent le même résultat, la première est plus rapide, par exemple, si dans votre exercice, vous avez 16 personnes ayant 20 ans, elle vous évite de passer par l'addition, et vous permet d'utiliser la multiplication (au lieu d'additionner "20" 16 fois, vous multipliez 16*20).

Exemple: 
Soit un groupe de 10 personnes dont les dates de naissance sont:
1954, 1970, 1983, 1975, 2001, 1975, 2002, 2002, 1982, 2009

Etape 1:
En 2012
Les personnes ont l'âge suivant:
1961-----51 ans
1970-----42 ans
1983-----29 ans
1975-----37ans
2001-----11 ans
2002-----10 ans
1982-----30 ans
2009-----3 ans

Etape 2:
51 ans----- 1 personne
42 ans----- 1
29 ans----- 1
37 ans----- 2
11 ans----- 1
10 ans----- 2
30 ans----- 1
3 ans-------1

Etape 3: 
Calculer l'âge moyen:
Somme (âge * nombre de personnes ayant cet âge) / nombre total de personnes du groupe (N)

Ici N=10

(51* 1) + (42*1) + (29*1) + (37*2) + (11*1) + (10*2) + (30*1) + (3*1)
= 260

260/ 10= 26

L'âge moyen du groupe est 26 ans.

Comment calculer la médiane

Pour calculer la médiane, il faut chercher la "valeur du milieu" (dans une liste de nombre par exemple).

-Une astuce très simple pour savoir où se trouve la position de la valeur médiane est d'utiliser la formule suivante, (surtout lorsque vous avez un grand nombre de nombres):
(x +1) / 2 
 
Avec x= le nombre total de valeurs

Cette formule permet de savoir exactement où se trouve la position de la valeur médiane.


Par exemple:

I) Nombre impair de nombres
Trouver la médiane de la liste de nombres suivante:
8, 53, 28, 75, 32

a) La première étape consiste à ranger les nombres du plus petit au plus grand:
8-28-32-53-75

b) La seconde étape est de chercher la valeur du milieu, en utilisant la formule (x+1)/2.
Ici (x+1)/ 2= (5+1)/ 2= 3
Donc la valeur qui se trouve à la 3ème position est la valeur médiane, ici 32.


II) Nombre pair de nombres
Maintenant, si vous avez un nombre pair de nombres:
8, 53, 28, 102, 43, 65

a) La première étape consiste à ranger les nombres du plus petit au plus grand
8-28-43-53-65-102

b) La seconde étape consiste à utiliser la formule (x+1)/ 2 pour déterminer la position de la valeur médiane.
(x+1) /2 = (6+1)/ 2 = 3.5

La valeur médiane est la valeur qui se trouve à la 3.5ème position de la liste de nombre.

Ici la valeur médiane est à cheval entre 43 et 53.


c) La troisième étape consiste à ajouter les deux valeurs trouvées et à les diviser par 2
(43+ 53)/ 2= 48

La valeur médiane pour cette liste paire de nombres est 48.


A noter
Cette formule (x+1)/2  pour rechercher la position de la valeur médiane  prend tout son sens lorsque l'on a une longue liste de nombres, comme par exemple:
2, 5, 6, 7, 9, 11, 15, 16, 19, 24, 39, 45, 102, 145, 167, 180, 203, 256, 307, 345, 490,....

Transformer une fraction en pourcentage

Pour transformer une fraction en pourcentage il suffit de diviser le nombre supérieur (numérateur) par le nombre inférieur (dénominateur).

Méthode 1

Prenons un exemple simple:
Comment transformer 9/10 en pourcentage.

Avec la calculatrice 9/10 donne 0.9, et quand vous multiplier ce nombre par 100, vous obtenez 90%. Vous devez ajouter le "%" pour que le lecteur puisse savoir que c'est un pourcentage.


Méthode 2

Il existe une autre méthode de calcul de pourcentage:

Parce que "pour cent" signifie "par 100", vous pouvez essayer de convertir la fraction pour obtenir une autre fraction " nombre / 100" en suivant ces étapes:

Etape 1: trouver un nombre par lequel multiplier la valeur du bas de la fraction (dénominateur) pour obtenir 100.
Etape 2: multiplier le nombre supérieure (numérateur) et le nombre inférieure (dénominateur) de la fraction par ce nombre.
Etape 3: ensuite, écrire juste le chiffre du haut avec le signe «%».

Exemple:
Exprimer la fraction 5/8 en pourcentage 

Etape 1:

Etape 2:

Etape 3:

Soit vous utilisez la méthode 1 soit la méthode 2, elles vous permettront d'arriver au même résultat lorsque vous essayez de transformer une fraction en pourcentage.

comment calculer le volume d'une boite

Pour calculer le volume d'une boite, il faut avoir les 3 dimensions.
La longueur
la largeur
la hauteur

et appliquer la formule correspondante.

-Si vous avez la boite, mesurez-la simplement. Ne vous inquiétez pas de savoir à quelle mesure vous attribuez le terme longueur, largeur ou hauteur (en tout cas, si vous n'êtes pas un scolaire ou lycéen). Dans le cas, où vous en seriez un, il vaut mieux examiner la boite et déterminer, selon les cours, ce qui pourrait être la longueur, la largeur et la hauteur.

longueur= 10 cm =L
largeur= 5 cm= l
hauteur=4 cm= h









Pour avoir le volume, il suffit de multiplier les 3 mesures:
L*l*h=10cm* 5cm* 4cm= 200cm^3.

Sur internet, il est possible de trouver beaucoup de calculatrice gratuite qui peuvent également vous aider à calculer le volume d'une boite.

comment calculer la tva

Pour savoir comment calculer la TVA, il suffit de connaitre le prix hors taxe (HT) ou le prix toutes taxes comprises (TTC), ainsi que le taux de TVA.


Attention il faut d'abord savoir si le prix du produit est hors taxes (HT) ou taxes comprises (TTC), cela détermine le calcul à faire.

Vous pouvez soit utiliser un coefficient multiplicateur ou soit utiliser le taux de tva directement, mais quelque soit la méthode le résultat est le même.

1) Comment calculer la tva avec un prix hors taxe?

• Avec le coefficient multiplicateur

Si la tva est de 19.6%, le coefficient multiplicateur est 1,196
Si la tva est de 8.5%, le coefficient multiplicateur est 1,085
Si la tva est de 7%, le coefficient multiplicateur est 1,070
Si la tva est de 5.5%, le coefficient multiplicateur est 1,055

Exemple:

-Montant hors taxe= 150 

-Taux de tva=19,6%

Calcul de la tva:

150*1,196= 179,4 = montant toutes taxes comprises

Montant de la tva= Montant TTC-Montant HT
Montant de la tva=179,4-150= 29.40   

• Avec le taux de tva appliqué directement au montant hors taxes

Exemple:

-Montant hors taxe= 150 

-Taux de TVA=19,6%

Calcul de la tva:

Montant de tva= 150*19,6/100 =29.40

Et si vous coulez le montant TTC, il est égal au:
Montant HT+ Montant de la TVA= 150+29,40=179,40.

 

2) Comment calculer la tva avec un prix taxes incluses (TTC)?

• Avec le coefficient multiplicateur

Si la TVA est de 19.6%, le coefficient multiplicateur est 1/1,196
Si la TVA est de 8.5%, le coefficient multiplicateur est 1/1,085
Si la TVA est de 7%, le coefficient multiplicateur est 1/1,070
Si la TVA est de 5.5%, le coefficient multiplicateur est 1/1,055

Exemple:

-Montant TTC=150

-Taux de tva=5,5%

Calcul de la tva:
Montant HT=Montant TTC * (1/1,055)= 150* (1/1,055)=142,18
Montant de TVA=Montant TTC-Montant HT= 7,82



Pour calculer la tva, il suffit de connaitre les données en main, notamment si vous avez un montant HT ou un montant TTC, en fonction de cela vous procédez au calcul avec le taux de TVA.
Le taux de TVA est le nombre exprimé en pourcentage, qui appliqué à un montant vous donne le montant de la TVA.
Ces calculs sont basiques mais sont importants notamment en comptabilité pour les différents calculs de TVA.

Comment calculer la diagonale d'un carré

Pour savoir comment calculer la diagonale d'un carré, nous allons procéder par étape pour t'aider à comprendre:

Tout d'abord, il te faut connaitre:
1) Le théorème de Pythagore.

    prend ton livre et relis le théorème de Pythagore, (même s'il traite du triangle rectangle).

2) La longueur du côté de ton carré.


Avec ces 2 éléments tu peux calculer la diagonale d'un carré.

Maintenant tu te dis:
'Le théorème de Pythagore traite du triangle rectangle mais moi je veux la formule avec le carré'.


Ce que tu as oublié c'est qu'un carré est un rectangle avec ab=cd=bd=ac

Regarde ce carré quand tu le tires vers la droite tu obtiens un rectangle.
Et si tu imagines que tu tires une ligne allant d'un angle à l'angle opposé, tu obtiens 2 triangles rectangles.

Voilà, si tu regardes bien tu constates que tu as un triangle rectangle en b qui est abd, et un second triangle rectangle acd, rectangle en c.






Exemple
Tu as un carré ABCD, avec AB=5cm

Comme cela a été dit plus haut AB=AC=CD=BD
Maintenant utilisons le théorème de Pythagore qui dit:

AD² =AC² + CD²

Toi, tu recherches AD uniquement, AD² va te permettre de trouver AD.

AD²=5² +5²












Donc la diagonale recherchée a une longueur correspondant à 7,07 cm (avec la calculatrice)


Si la simplification est dans ton programme, tu devras simplifier le résultat:

Voilà, tu as tout les éléments pour te permettre de savoir comment calculer la diagonale d'un carré.
-Si tu as la longueur du côté et si tu connais et applique le théorème de Pythagore, tu trouveras la diagonale du carré facilement.

Comment calculer un pourcentage

Pour savoir comment calculer un pourcentage, vous pouvez lire l'explication simple donnée ci-dessous:

Il faut savoir qu'un pourcentage peut s'écrire sous 3 formes qui correspondent à la même chose en terme de calcul, exemple:

a) 23 %

b) 23

   100

c) 0.23 (forme décimale).

Au lieu de dire "il a lancé 23 jetons sur 100," nous disons "il a lancé 23% de ses jetons.
Autrement dit, sur un nombre total de 100, 23 jetons ont été lancés.

Aussi , pour cent (%) signifie "pour chaque 100" ou "sur 100".
Le symbole (%) est un moyen rapide d'écrire une fraction avec un dénominateur de 100.


-Comment calculer un pourcentage?
Prenons un exemple simple:

A) Sur 48 étudiants, 12 sont des filles? Quel est le pourcentage de filles?

Puisque l'on n'a pas 100 étudiants (on en a 48), il faut tout ramener sur 100 (c'est à dire, le nombre de filles et le nombre d'étudiants.


Vous pouvez procéder ainsi, le résultat reste le même quelque soit la méthode utilisée:
12  x 100  = 25  ou  12 x 100 : 48  (avec la calculatrice, le résultat est 25).

48

25% représente le pourcentage recherché, la réponse est 25% d'étudiants sont des filles.

B) Et si la question est de calculer le pourcentage de garçons.
*Soit vous vous dites , si sur 48 étudiants il y a 12 filles, donc le reste est des garçons (eh oui).
donc 48-12=36 garçons.
et vous faites exactement le même calcul du dessus avec 36 garçons au lieu de 12 filles.

36   x 100  ou 36 x 100 : 48 (le résultat est 75 avec la calculatrice).

48

Donc il y a 75% de garçons parmi les étudiants.

*Soit vous faites le calcul avec le nombre de filles (comme au dessus), dans ce cas, vous obtenez le pourcentage de filles (25%). A ce moment, vous vous dites, que le reste est des garçons.
Donc sur 100 étudiants, si vous avez 25 filles, donc les 75 autres sont des garçons (100-25=75)
Donc il y a 75% de garçons parmi les étudiants.


12  x 100  = 25  ou  12 x 100 : 48  (avec la calculatrice, le résultat est 25).

48

100-25=75

Donc 75% des étudiants sont des garçons.

Voilà j'espère que maintenant vous savez comment calculer un pourcentage.

Comment calculer l'aire d'un triangle rectangle

Si tu veux savoir comment calculer l'aire d'un triangle rectangle, je t'encourage à lire la suite:

Il te suffit tout simplement de:
A- multiplier la longueur par la largeur, si les 2 unités sont les mêmes, sinon
B- tu dois d'abord faire une conversion et ensuite multiplier la longueur par la largeur (et mettre aussi l'exposant, comme dans l'étape A).


EXPLICATION SCHEMATIQUE

A- multiplier la longueur par la largeur, si les 2 unités sont les mêmes (surtout n'oublie pas de multiplier l'unité utilisée, en mettant l'exposant).

Si L=10 cm et l=5 cm
     l'aire du triangle rectangle sera:
     L x l= 10cm x 5cm = 50cm²










B-tu dois d'abord faire une conversion et ensuite multiplier la longueur par la largeur

 L= 90 mm
 l = 4 cm

 L x l = 90mm x 4cm     NON IMPOSSIBLE!









Si la question est comment calculer l'aire du triangle rectangle en mm, tu dois convertir la dimension exprimée dans l'autre mesure en mm (dans cet exercice cela veut dire, convertir la largeur en mm).

l=4cm=40mm
L=90mm (cela ne change pas)
L'aire du triangle rectangle est L x l= 40mm x 90mm=3600mm²


Si au contraire la question est comment calculer l'aire du triangle rectangle en cm, tu dois convertir (pour cet exercice) la longueur en cm.
L=90mm= 9cm
l=4cm (ne change pas)
L'aire du triangle rectangle est L x l=9cm x 4cm=36cm²



Maintenant, j'espère que tu as compris comment calculer l'aire d'un triangle rectangle.

Comment calculer l'aire d'un rectangle

Comment calculer l'aire d'un rectangle?
Si tu es ici, c'est une question que tu te poses, je vais t'expliquer certainement des choses que tu connais déjà et que tu as certainement oublié.

Il faut s'intéresser à 2 choses:
1- les nombres donnés (c'est le plus simple, il suffit de les multiplier) ET
2- l'unité de mesure (le multiple/sous-multiple) utilisé (si on peut dire cela, c'est le plus important-  est-ce que tu as affaire à des cm, des mm, des dam, km...)
      A- si l'unité (ou le multiple/sous-multiple) est la même pour la longueur et la largeur, il suffit de multiplier l'unité de mesure (ou le multiple/sous-multiple) également, en ajoutant un exposant.
      B- si l'unité de mesure (ou le multiple/sous-multiple) est différente pour la longueur et la largeur, il faut faire une conversion, en utilisant un tableau de conversion.


EXPLICATION SCHEMATIQUE

1- les nombres donnés (c'est le plus simple, il suffit de les multiplier)

Aire d'un rectangle est:
L (longueur) x l (largeur)


Exemple:



Si
L=6
l=5
L' aire de ce rectangle sera Lxl=6x5=30.

2- l'unité (ou le multiple/sous-multiple) de mesure utilisée (si on peut dire cela, c'est le plus important-  est-ce que tu as affaire à des cm, des mm, des dam, km...).

 
A-
Si l'unité est le cm:



L=6cm
l=5cm
L'aire de ce rectangle sera:
6cm x 5cm=  30cm²





Autre exemple

Si l'unité est le mm:


L=6mm
l=5mm

L'aire de ce rectangle sera:

6mm x 5mm= 30mm²

B-
Maintenant si tu as des unités (multiple/sous multiples) de mesure qui ne sont pas les mêmes tu dois convertir l'une des unités dans l'autre unité pour pouvoir faire le calcul.
Tout d'abord tu auras besoin de faire une conversion

Exemple:
L=6cm
l=5mm

Si tu dois trouver l'aire du rectangle en cm, tu dois convertir 5mm en cm.
5mm=0.5cm

 6 cm x 5mm = NON

CONVERSION NECESSAIRE
5mm=0.5cm

L'aire du rectangle est 6cm x0.5cm=3cm²


RESUME
Il suffit de multiplier les nombres et de multiplier l'unité utilisée si elles sont les mêmes, sinon tu fais une conversion pour avoir la même unité et tu multiplie ainsi, les deux unités.
Voilà comment se calcule l'aire d'un rectangle.